开立方根的方法和步骤
1、将被开立方数的整数部分从个位起向左每三位分为一组。
2、根据最左边一组,求得立方根的最高位数。
3、用第一组数减去立方根最高位数的立方,在其右边写上第二组数。
4、用求得的最高位数的平方的300倍试除上述余数,得出试商;并把求得的最高位数的平方的300倍与试商的积、求得的最高位数的30倍与试商的平方的积和试商的立方写在竖式左边,观察其和是否大于余数,若大于,就减小试商再试,若不大于,试商就是立方根的第二位数。
5、用同样方法继续进行下去。

扩展资料:
一、开根号方法
1、数m开n次方,n位一节为一根,前根均作a,a后需求的根均作b;前根a的位数不断增长,后根b永远作一位根视;直至开尽或开至所需要的位数。
2、首位a根用1~9内n方诀直接确定(随后就无a根系列的事了;或用双根或多位根作a;即将约小于被开数的乘方数的幂底整数值作为a根,再求b=x),b根用“标准固律方程式”或“简易求b方程式”求。
二、快速开根
从个位起向左每隔两位为一节,若带有小数从小数点起向右每隔两位一节,用逗号分开求不大于左边第一节数的完全平方数为商,再从左边第一节数里减去求得的商,在它们的差的右边写上第二节数作为第一个余数再把商乘以20,试除第一个余数,所得的最大整数作试商用商乘以20加上试商再乘以试商。
如果所得的积小于或等于余数,就把这个试商写在商后面,作为新商;如果所得的积大于余数,就把试商逐次减小再试,直到积小于或等于余数为止;用同样的方法,继续求。
参考资料来源:百度百科-开立方
参考资料来源:百度百科-开根
所有立方根公式
立方公式如下:
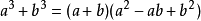
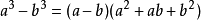
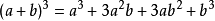
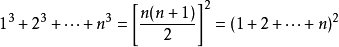
扩展资料:
1、性质
(1)在实数范围内,任何实数的立方根只有一个
(2)在实数范围内,负数不能开平方,但可以开立方。
(3)0的立方根是0
(4)立方和开立方运算,互为逆运算。
(5)在复数范围内,任何非0的数都有且仅有3个立方根(一实根,二共轭虚根),它们均匀分布在以原点为圆心,算术根为半径的圆周上,三个立方根对应的点构成正三角形。
(2)在复数范围内,负数既可以开平方,又可以开立方。
2、大小比较
具有大小意义的数字大小比较中:
(1)做这两个数的立方,立方数大者大
(2)作差,两数相减,若差大于0,则被减数大;若差小于0,则减数大;若差等于0,则一样大;
(3)比较被开方数,立方根大者大
参考资料:百度百科-立方根
如何手算开立方根
一、分为整数开平方和小数开平方。
1、整数开平方步骤:
(1)将被开方数从右向左每隔2位用撇号分开;
(2)从左边第一段求得算数平方根的第一位数字;
(3)从第一段减去这个第一位数字的平方,再把被开方数的第二段写下来,作为第一个余数;
(4)把所得的第一位数字乘以20,去除第一个余数,所得的商的整数部分作为试商(如果这个整数部分大于或等于10,就改用9左试商,如果第一个余数小于第一位数字乘以20的积,则得试商0);
(5)把第一位数字的20倍加上试商的和,乘以这个试商,如果所得的积大于余数时,就要把试商减1再试,直到积小于或等于余数为止,这个试商就是算数平方根的第二位数字;
(6)用同样方法继续求算数平方根的其他各位数字。
2、小数部分开平方法:
求小数平方根,也可以用整数开平方的一般方法来计算,但是在用撇号分段的时候有所不同,分段时要从小数点向右每隔2段用撇号分开。
如果小数点后的最后一段只有一位,就填上一个0补成2位,然后用整数部分开平方的步骤计算。
二、
1.根据平方和(立方和)公式手算开平方(开立方)。以往初中教材上必学的手算开平方就是此法,开立方也可类似处理。
2.利用二分法以及不等式两边夹,如求2的平方根
1)1^2<2<2^2
2)(1.4)^2<2<(1.5)^2
......
此法运算量大。
3.利用微分求近似值——由于此法误差不可控,可结合前一方法逐步提高精度,计算量比前一方法小。
4.原始的泰勒展开,计算量大,误差可控。
5.变形的泰勒展开,计算方法里的。

参考链接:数学资源
立方根怎么算
如果一个数的立方等于a,那么这个数叫a的立方根,也称为三次方根。也就是说,如果x³=a,那么x叫做a的立方根。
注意:在平方根中的根指数2可省略不写,但立方根中的根指数3不能省略不写。
举例说明如下:
2的立方等于8,所以8的立方根是2。
扩展资料
立方根的性质:
(1)在实数范围内,任何实数的立方根只有一个
(2)在实数范围内,负数不能开平方,但可以开立方。
(3)0的立方根是0
(4)立方和开立方运算,互为逆运算。
(5)在复数范围内,任何非0的数都有且仅有3个立方根(一实根,二共轭虚根),它们均匀分布在以原点为圆心,算术根为半径的圆周上,三个立方根对应的点构成正三角形。
(6)在复数范围内,负数既可以开平方,又可以开立方。